Area Moment of Inertia
I'll keep this short. Few things are more boring (but complicated) than the "Area Moment of Inertia" or the "Moment of Inertia". Mathematically those two entities are almost the same, physically they are quite different. And both of them are absolutely crucial to sword performance.
First things first: When you bend something elastically, there is always a neutral axis. Look it up here. The parts of whatever you bend that are farthest away from this neutral axis experience more strain than the parts close to it. So if you distribute a given amount of material in such a way that most of it is far away from the neutral axis, it will be more difficult to bend than if most of it is close to the axis. A thin-walled tube in comparison to a solid rod is a good example for that.
The major result we got in the module considering bending a beam with any constant cross-section was the following situation / equations
 
   
Calculating beam bending
First example for calculating a deflection line
The coordinate system has been adjusted to make the results easy (e.g. no minus signs).
   
zmax(x = 0)   =    F · l03
3Y · IA
     
F is the applied point force at the end of the beam, l0 is the length of the beam, Y is Young's modulus of the (homogeneous) material in use, and IA is the area moment of inertia containing all information about the cross-sectional geometry of the beam relative of the direction of bending. zmax is the maximum deflection, it varies inversely with the area moment of inertia.
How do we calculate the area moment of inertia? Let's look at a simple case, a rectangular beam:
     
Aerea momentum; calculation
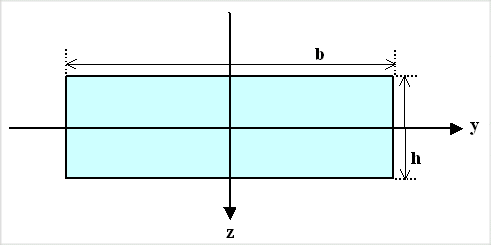First example for calculating an area moment of inertia
     
  Now apply a force in the z-direction, It bends this rod downwards in the z-direction. For this case I then need the area momentum Iy of the rod. The index is "y" because the vector going with the torque or momentum for bending lies in in the y-axis. Bending in y- direction needs Iz. The two area momentums Iy and Iz are defined by:
     
   
Iz   =      
  ó
   õ
Area 		y2 · dA
       
Iy   =      
  ó
   õ
Area		 z2 · dA
     
  Let's do one momentum, just for the hell of it:
     
I z   =     z ' = +b/2
     ó
      õ
z' = - b/2		    y  ' = h/2
     ó
      õ
y' = - h/2		   y2 · dz · dy
             
   =     1/3y3 y ' = +b/2
     |
     |
y ' = - b/2		  ·  z z' = +d/2
     |
     |
z' = - d/2		  =     1/12 b3 · d
             
             
     
For Iy we get Iy = 1/12 d3 · b, of course. So there is nothing to it. At least as long as the shape of your area is not too complicated.
Of course in real life sword cross-sections are not rectangular but tend to be more complicated. Doing the integrals then can be cumbersome.
Since engineers are resourceful people, they found ways to make life easier. You might, for example, describe your complicated area by "tiling" it with simple forms with known area moment. Then you construct the area moment of your complex shape by "adding up" in a certain way the area moments of the tiles.
All we need to know is that obtaining the area moments of your sword cross-sections is not a problem. Here are a few examples.
   

With frame With frame as PDF

go to Galileo Galilei

go to Bending of Beams

go to Bending of Beams - Full Theory

go to 12.2. Static Sword Properties; 12.2.1 Sword Bending

go to Moment of Inertia

go to 12.2.5 Sword Types and Static Properties

go to 12.3 Dynamic Properties; 12.3.1 Moving a Stick

go to Buckling

go to 12.2.3 Sword Buckling

© H. Föll (Iron, Steel and Swords script)